Triangles rectangles ( Pythagore )
I Cercle circonscrit à un triangle
rectangle
Le
triangle ABC est rectangle en A
On appelle hypoténuse
d'un triangle rectangle, le coté qui est opposé
à l' angle droit : c'est le plus grand coté
du triangle.
1ère
Propriété : Le centre du cercle circonsrit à un triangle
rectangle est le milieu de l' hypoténuse. On peut aussi dire que le
triangle rectangle est inscriptible dans un cercle dont un diamètre
est l'hypoténuse.
2ème Propriété
: Dans un triangle rectangle, la médiane issue du sommet de l' Angle
droit mesure la moitié de l'hypoténuse.
II Angles droits sans équerre
1ère Réciproque
: Si on joint un pint d'un cercle aux extremités d'un diamètre,
alors on obtient un triangle rectangle
2ème réciproque
: Si une médiane d'un triangle mesure la moitié du coté
qui lui correspond alors ce triangle est réctangle
III Activité de Pythagore
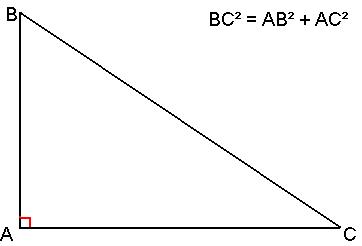
Propriété de
Pythagore : Dans un triangle rectangle, le carré de l'hypoténuse
est égal à la somme des carrés des cotés de l'
angle droit
IV Méthodes et Modèles
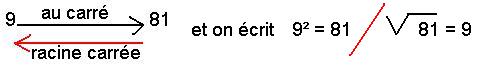
Pour utilise la propriété de
Pythagore on peut demander de claculer un coté d'un triangle rextangle
en donnant les mesures des 2 autres
1er Modèle
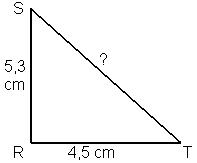Dans
le triangle rectangle RST rectangle en R, je peux appliquer la propriétée
de Pythagore : ST² = RS² + RT²- ST² = 5,3² + 4,5²
- ST² = 48, 34
- donc
- ST =
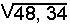( valeur exacte )
- donc ST
7,0
cm ( valeur approchée arrondie au 1/10 ou au mm près =
2ème Modèle
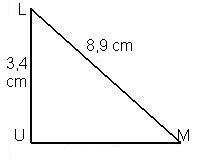Dans
le triangle ULM rectangle en U, je peux appliquer la propriétée
de Pythagore : LM² = UL² = UM²- 8,9² = 3,9² + UM²
- 79,21 = 15,21 + UM²
- donc
- UM² = 79,21 - 15,21
- UM² = 64
- UM =
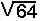
- UM = 8 cm ( valeur exacte )
V Réciproque de Pythagore
Nous admetons sans démonstration que si le carré
du grand coté d'un triangle est égal à la somme des carrés
des 2 autres côtés alors ce triangle est réctangle
1er Modèle
Le triangle LMN tel que : LM : 5cm / MN : 12 cm / LN : 13
cm ----> est il rectangle ?
- LN² = 13² = 169
- LM² + MN² = 5² + 12² = 25 + 144 = 169
- Je constate que LN² = LM² + MN²
- Je conclus d'après la propriété de Pythagore
que le triangle est rectangle en M
2ème Modèle
Le triangle ABC tel que : AB : 2,5cm / BC : 7cm / AC : 6 cm
----> Est il rectangle ?
- BC² = 7² = 49
- AB² + AC² = 2,5² + 6² = 6,25 + 36 = 42,25
- Je constate que BC² n'est pas égal à AB²
+ AC²
- Je conslus, d'après la propriété de
Pythagore que le triangle ABC n'est pas rectangle
