Nombres relatifs
I Aditions
1) Mêmes signes
- Pour additionner deux nombres de même
signe , on ajoute et on prend le signe commun
- Exemples : ( + 3 ) + ( + 5 ) = 3 + 5 = 8
/ ( - 3
) + ( - 5 ) = - 3 - 5 = - 8
2) Signes contraires
- Pour additionner deux nombres de signes contraires , on soustrait
et on prend le signe du plus grand nombre :
- Exemple : ( - 3 ) + ( + 5 ) = 2
II Soustractions
- Pour soustraire un nombre, j'ajoute son opposé
- Exemples :
- Soustraire + 5 : 3 - ( + 2 ) = 3 +
( - 5 ) = - 2
- Soustraire + 5 : ( - 3 ) - ( + 5 ) = ( -
3 ) + ( - 5
) = - 8
- Soustraire - 5 : 3 - ( - 5 ) = 3 +
( + 5 ) = 8
- Soustraire - 5 à - 3 : ( - 3 ) - ( - 5 ) = ( -
3 ) + ( + 5
) = 2
Retenir : - + = - / - - = +
III Comparaisons
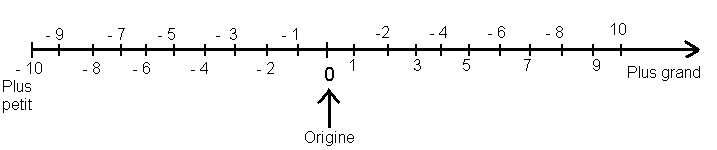
Plus les nombres négatifs s'éloignent
de l'origine plus ils sont petits
IV Multiplications
1 ) Nombres de même signe
- Le produit de 2 nombre de même signe est positif
- Exemples : 3 x 5 = 15 / ( - 3 ) x ( - 5 ) = 15
2 ) Nombres de signes contraires
- Le produit de 2 nombres de signes contraires est négatif
- Exemples : 3 x ( - 5 ) = - 15 / ( - 3 ) x 5 = - 15
V Multiplications de 3 nombres ou plus
- 1 ) Si le produit comprend un nombre pair de facteurs négatifs,
alors, il est positif ( ex : ( - 2 ) x 3 x ( -5 ) = 30 )
- 2 ) Si le produit comprend un nombre impair de facteur négatif,
alors il est négatif ( ex : ( -2 ) x 3 x ( - 5 ) x ( - 4 ) = - 120
VI Divisions
1 ) Equation égalité avec x
- 2x = 12 donc x = 6 = 12/2
- - 2x = - 12 donc x
= 6 = -12/-2
- -2x = 12 donc x = -6
= 12/-2
- 2x = -12 donc x = -6
= -12/2
2 ) La règle des signes
- Les quotients ont la même règle des signes que
les produits
3 ) Signe du quotient
- 12/-2 = -12/2 = - ( 12/2 )
- -12/2 = 12/2
4 ) 3 sortes de quotients
- Nombre Entier : -12/-2 = 6 ----> valeur exacte
- Nombre Décimal : -12/16 = 0,75 ----> valeur exacte
- Nombre rationnel : -2/-12 divisé par 4 = 1/6
- Si on demande de donner une valeur approchée, on doit
preciser si on veut une troncature ou un arrondi et à quel ordre.
|
valeurs approchées de 1/6
|
à l' unité
|
au 1/10e
|
au 1/100e
|
au 1/1000e
|
|
Troncature
|
0
|
0,1
|
0,16
|
0,166
|
|
Arrondi
|
0
|
0,2
|
0,16
|
0,167
|
VII Les inverses
1 ) Comment trouver un inverse
2 ) A quoi sert un inverse ?
- Un inverse sert à calculer mentalement
- Pour multiplier ont peut diviser par son inverse : 8 x 0,25
= 8 / 4 = 2
- Pour diviser on peut multiplier par son inverse :
130 / 0,01 = 130 x 100 = 13 000
VIII Priorités
- Pour calculer une expression, il faut comencer par les calculs
qui sont écrits entre les parenthèses ou la ou il y a une grand
trait de fraction , ensuite on calcule les multiplications et les divisions
Exemples :
- - 2 - 3 x ( - 1 + 5 ) = - 2 - 12 = -
14
- - 9 + 15
/ - 5 = - 9 + ( - 3 )
IX Formules
- ( a + b ) x c ----> produit factorisé = a x c +
b x c ----> somme dévelopée
Calculer :
- 1ère facon :

- 2ème facon :

X Valeur numérique d'une expression littérale
Calculer chacune des expressions suivantes pour A = - 9 /
B = 2 / C = - 5
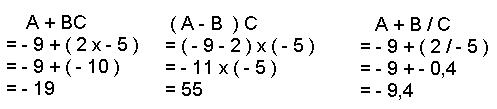
L'inverse
d'un négatif est aussi négatif